Tau Appearance Measurement
This analysis investigates tau neutrino appearance from atmospheric neutrino oscillations using ANTARES. It evaluates reconstruction algorithms, implements quality cuts, and uses a profile likelihood approach to assess sensitivity to the νμ→ντ oscillation channel.
Overview
This analysis investigates the feasibility of detecting tau neutrino ($\nu_\tau$) appearance in the ANTARES neutrino telescope using 15 years of simulated events. The study focuses on low-energy (10–100 GeV) up-going neutrinos, where neutrino oscillation effects are most significant.
Key Components
Neutrino Oscillation Context
Atmospheric neutrinos provide a natural beam for studying neutrino oscillations over a wide range of baselines and energies. The following key aspects define the oscillation context:
- Atmospheric neutrinos initially consist of $\nu_e$ and $\nu_\mu$ only
- $\nu_\tau$ appearance is solely due to neutrino oscillations ($\nu_\mu \to \nu_\tau$)
- One of the maxima in the oscillation probability for muon neutrinos occurs at $\sim 20$–$30\ \text{GeV}$ for vertically up-going events
Three-Flavor Oscillation Probability:
The $\nu_\mu \to \nu_\tau$ transition probability is given by:
$$ P(\nu_\mu \to \nu_\tau) = 4|U_{\mu3}|^2|U_{\tau3}|^2 \sin^2\left(\frac{\Delta m_{31}^2 L}{4E}\right) + 8|U_{\mu3}U_{\tau3}U_{\mu2}U_{\tau2}|\cos\left(\frac{\Delta m_{31}^2 L}{4E}\right)\sin\left(\frac{\Delta m_{31}^2 L}{4E}\right)\sin\left(\frac{\Delta m_{21}^2 L}{4E}\right) $$where $U$ is the PMNS mixing matrix, $\Delta m_{ij}^2$ are mass-squared differences, $L$ is the baseline, and $E$ is the neutrino energy.
Tau Normalization Parameter:
$$ n_\tau = \frac{N_{\text{measured}}}{N_{\text{expected}}} $$Event Topologies
- Track-like events: $\nu_\mu$ CC interactions and $\nu_\tau$ CC decays to muons
- Shower-like events: $\nu_e$ CC, all NC interactions, and $\nu_\tau$ CC decays to hadrons/electrons
Reconstruction Algorithms Comparison
We evaluated three distinct algorithms for the event reconstruction, each with unique strengths and limitations for different event topologies and energy regimes with the aim of finding the most suitable for this analysis.
AAFit
- Traditional maximum likelihood fit optimized for high-energy tracks
- Poor performance for low-energy showers
- Energy overestimation in low-energy regime
- Only 13% of showers remain after quality cuts
BBFit
- Geometric reconstruction using detector lines as reference
- Better direction resolution than AAFit
- No energy reconstruction capability
- Moderate efficiency for both topologies
NNFit (Neural Network Fit)
- Machine learning approach with separate models for tracks and showers
- NNFitTrack: optimized for $\nu_\mu$ CC events
- NNFitShower: optimized for $\nu_e$ CC and NC events
- Provides error estimates for all reconstructed parameters
- Best direction resolution among all algorithms
- Low efficiency (19.5%) but high quality reconstruction
Cut Selection Strategies
To ensure reconstruction quality and minimize background contamination, we implemented specific selection criteria for each event topology based on reconstruction uncertainties. Several series of cut selection criteria were implemented with the “harshest” and “purest” among them being the following resulting in the smallest event sample.
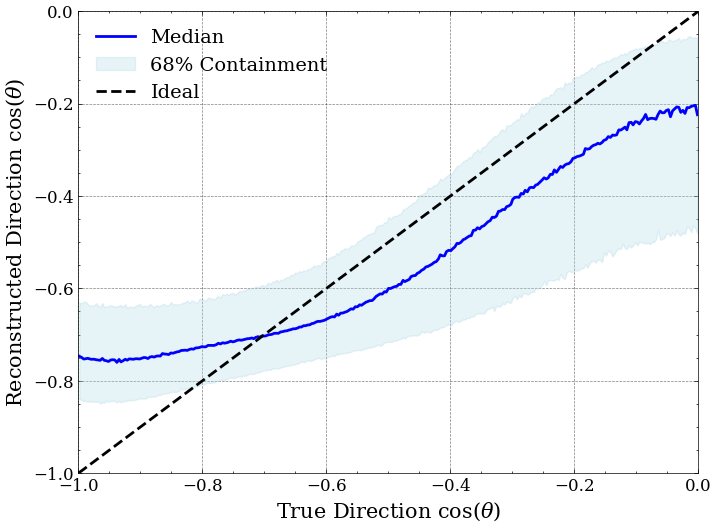
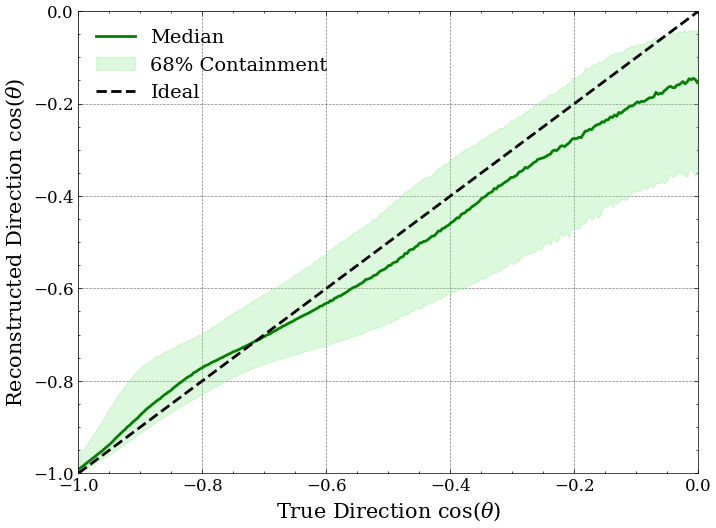
NNFit Quality Cuts
For tracks:
- $\sigma_{R,\text{closest}} < 10\ \text{m}$
- $\sigma_{Z,\text{closest}} < 10\ \text{m}$
- $\sigma_{\theta} < 8^\circ$
- $\cos\theta < -0.4$
For showers:
- $\sigma_{R,\text{vertex}} < 10\ \text{m}$
- $\sigma_{Z,\text{vertex}} < 10\ \text{m}$
- $\cos\theta < -0.4$
Statistical Analysis Method
$\chi^2$ Profile Likelihood Approach
The analysis uses a Poisson $\chi^2$ statistic to determine sensitivity to $\nu_\tau$ appearance:
\[\chi^2(\text{model}, \text{data}) = 2 \sum_{i,j} \left[ \left( n^{\text{model}}_{ij} - n^{\text{data}}_{ij} \right) + n^{\text{model}}_{ij} \cdot \ln \left( \frac{n^{\text{data}}_{ij}}{n^{\text{model}}_{ij}} \right) \right] + \sum_{\alpha} \left( \frac{\alpha_{\text{exp}} - \alpha_{\text{obs}}}{\sigma_\alpha} \right)^2\]Components:
- Statistical term: Poisson comparison between expected and observed events in each $(E, \theta)$ bin
- Systematic term: Penalty for nuisance parameters deviating from expected values
TauNorm Scanning Procedure
- Free fit: Find minimum $\chi^2$ with TauNorm unconstrained
- Fixed scan: Calculate $\chi^2$ for TauNorm values from 0 to 2
- $\Delta\chi^2$ calculation: $\Delta\chi^2 = \chi^2{\text{fixed}} - \chi^2{\text{free}}$
- Significance conversion: $\sigma = \sqrt{\Delta\chi^2}$
Asimov Dataset Approach
- Uses expected event counts without statistical fluctuations
- Ensures TauNorm converges to true value ($n_\tau = 1$ for standard oscillations)
- Provides median expected sensitivity
Sensitivity Results
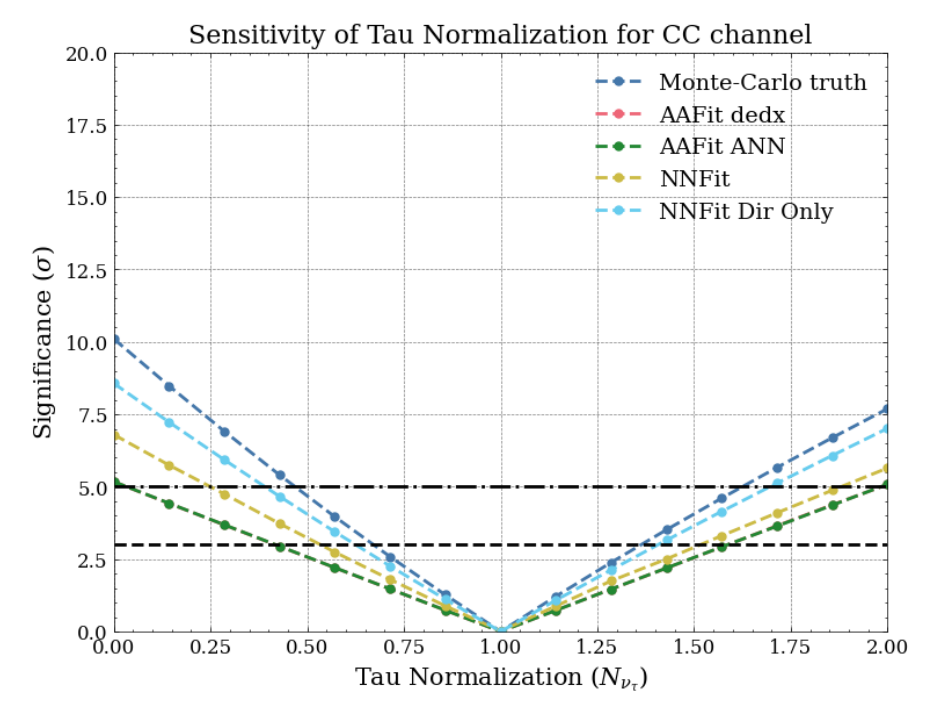
Algorithm Performance
- NNFit shows best sensitivity despite lower efficiency
- Challenges in energy resolution for $\nu_\tau$ appearance can be mitigated with proper binnnig
- Systematic uncertainties significantly impact sensitivity in full analysis
Key Challenges and Limitations
- Low reconstruction efficiency for $\nu_\tau$ events (especially with NNFit)
- Energy reconstruction difficulties below $70\ \text{GeV}$
- High atmospheric muon background requiring strict veto cuts
- Systematic uncertainties from flux models and cross-sections
- No particle identification capability in ANTARES
Conclusion
The analysis demonstrates ANTARES's potential to contribute to $\nu_\tau$ appearance measurements with significance exceeding $6\sigma$ for the chosen dataset and assumptions for the simplification of the problem. In the entire lifetime of the detector, after cut selection more than 300 $\nu_{\tau}$ under CC interactions with shower topology are present, providing more than enough statistics to warrant such an analysis. NNFit provides the best reconstruction performance despite efficiency limitations. The statistical approach using $\chi^2$profile likelihood with systematic uncertainties provides a robust framework for evaluating sensitivity to tau neutrino appearance.
.